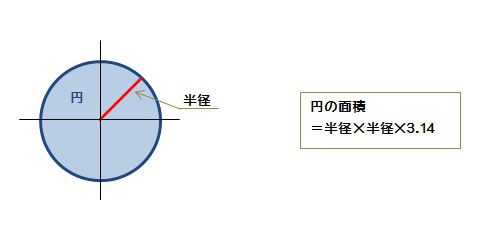
下の図は一般的な円です。

 

 

 

円の面積はどのように求めればよいでしょうか？
ここでも既に答えが分かっているかもしれませんが、同様に

 

 

なぜ、そうなるのか？

 

 

というのを一緒に考えてみてください。
ヒントは同じく「平行四辺形」です。

 

 

円で平行四辺形を作成することができるでしょうか？

 

 

と、考える前に今回の挑戦に必要となる式を１つ紹介します。
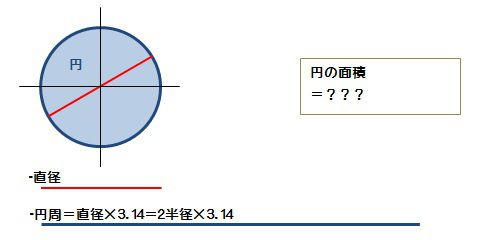
円の直径と円周の関係です。

 

 

円周＝直径×３．１４

 

 

この３．１４とはπ（パイ）と呼ばれる円周率です。
円周は直径の３．１４倍ということです。

 

 

「直径は半径の２倍」なので、これをさらに細かくすると

 

 

円周＝２×半径×３．１４

 

 

となります。
それでは、これを上手く利用していきましょう！

 

それでは、円を平行四辺形に変更させるために
まず円を「４等分」してから変形してみます。

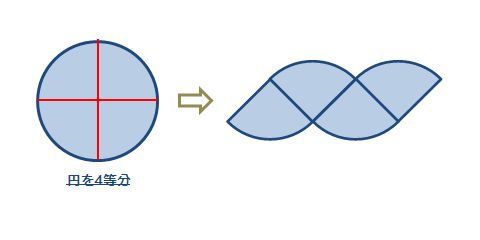
平行四辺形に見えるでしょうか？まだ、見えないですね。
それでは「８等分」してから変形してみましょう。

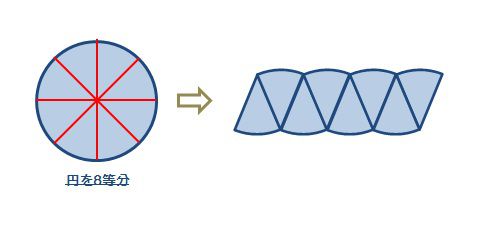
少し、平行四辺形に近づいてきました。
それでは「１６等分」してから変形してみましょう。

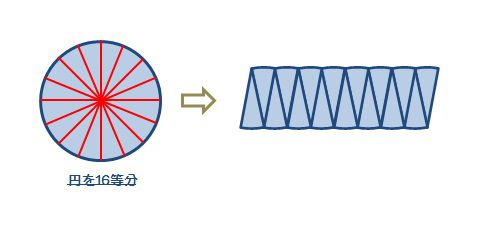
かなり、平行四辺形に近づきました。
この様に細かくしていけばいく程、平行四辺形にどんどん近づいきます。

 

 

つまり、円は平行四辺形に変形が可能ということです。
平行四辺形に変形させることができれば、もう計算はできると思います。

 

平行四辺形に変形させることができれば、今まで通り計算を進めていくだけです。
ただし、気をつけなければいけない部分があります。

 

 

平行四辺形の面積＝たて×よこ

 

 

今回、この『たて』と『よこ』をどのように置き換えられるでしょうか？

 

 

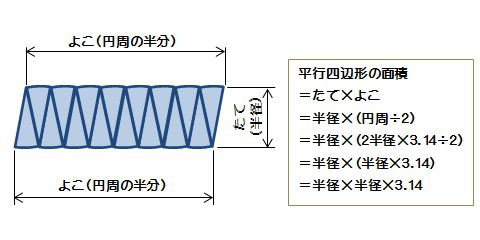
１６等分した図で考えてみると
『たて』は円の『半径』に置き換えられますよね？

 

 

また、
『よこ』は『円周の半分』に置き換えられますよね？

 

 

そして、円周は一番初めに説明したように
円周＝２×半径×３．１４で表せます。

 

 

なので、

 

 

円の面積＝平行四辺形の面積

 

＝たて×よこ

 

＝半径×円周の半分

 

＝半径×｛（２×半径×３．１４）÷２｝

 

 

と計算されて…

 

 

円の面積＝半径×半径×３．１４

 

 

となるのです＾＾