ここでは四角形以上の”多角形の内角の和”について考えてみましょう。
ではさっそく、
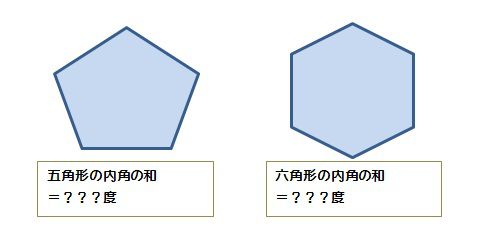
下に五角形と六角形の図があるので、それぞれの内角の和を考えてみましょう。
考え方は四角形の内角の和を求めるときと同じです。
多角形の中に三角形が何個作れるでしょうか?
算数の公式覚えてますか? > 図形の内角の和 > 多角形の内角の和
<スポンサードリンク>
ここでは四角形以上の”多角形の内角の和”について考えてみましょう。
ではさっそく、
下に五角形と六角形の図があるので、それぞれの内角の和を考えてみましょう。

考え方は四角形の内角の和を求めるときと同じです。
多角形の中に三角形が何個作れるでしょうか?
五角形と六角形の内部に作成できる「三角形の数」「内角の和」は下の図の通り。

四角形と同じように、三角形の数が分かれば内角の和は求められますよね^^
どうですか?ここまではそれほど難しくないと思います。
多角形と言っても、まだまだ五角形、六角形と数が少ない形ですからね。
ということで!ここで一気に「百角形」の内角の和を求めてみましょう。
びっくりだと思いますが、下に今までの値を表にしたので参考にして下さい。
ある法則になってるので、それが分かればすぐに答えが導けます。
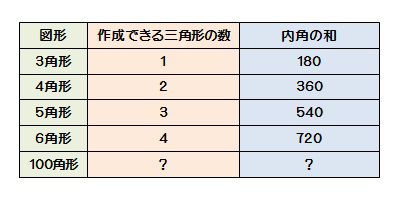
法則がわかりましたか?
もう少し詳しいヒントをだしますね。赤字は表内の数値を導き出した計算式です。

ここまでくると、もう分かると思います。
答えはこのようになります。
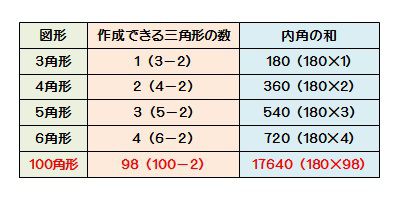
これで、どんな多角形でも内角の和は計算することができますね!
でも、この表を覚えておかないといけません…。
そこで考えるのが公式!!!
法則に従った計算式を作ってみましょう。
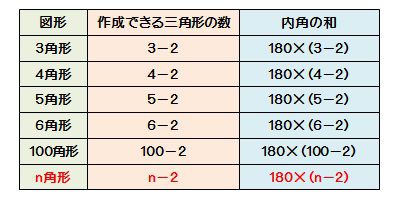
上の表は計算式のみが書いてあります。見れば分かると思いますが
・n角形の時
・その内部に作成できる三角形の数:(n−2)個
・その内角の和:180×(n−2)度
という意味です。
試しに数値を代入して確認してみましょう。
・五角形の場合:n=5
・内部に作成できる三角形の数:n−2=5−2=3個
・内角の和=180×(n−2)=180×(5−2)=540度
どうですか?五角形の内角の和は540度で間違いないですよね?
したがって、
n角形の内角の和=180×(n−2)
となるのです。これが公式ですよ^^
n角形の内角の和=180×(n−2)
この公式を忘れてしまったらどうしたらよいでしょうか?
多角形の内角の和は求められないでしょうか?
そんなことはありません。
忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。

三角形、四角形、五角形辺りまでで、
「作成できる三角形」と「内角の和」の関係を表にすれば、法則を思い出せると思います。
もちろん、
その法則でこの公式が導き出されていることを理解していないダメですよ。
公式だけではなく、そこに至るまでの経緯もしっかり理解しておきましょう。
<スポンサードリンク>
算数では様々な公式を覚えます。しかしその公式の意味を知っている方は多くないと思います。本ホームページでは公式の意味や公式の導き方を図を使用して分かりやすく説明しています。 これで計算するのが楽しくなるかもしれませんよ。
Copyright 算数の公式覚えてますか? All Rights Reserved.